Hi,
I am trying to understand static Smagorinsky model implemented in Palabos. As described in the documentation:
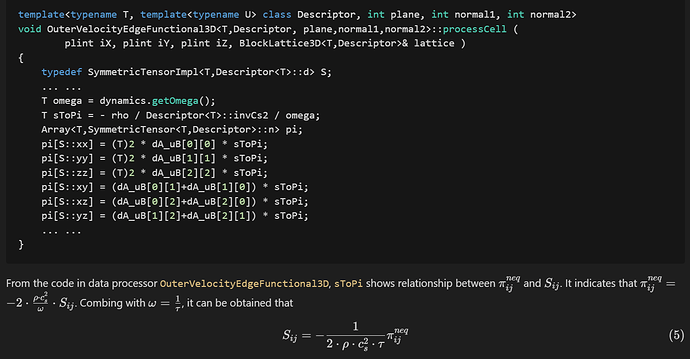
I could understand this from the relationship between the stress tensor and strain rate: Pi[sup]neq[/sup]=-2c[sub]s[/sub][sup]2[/sup]rhotau*S.
However, when I look at the file /complexDynamics/smagorinskyDynamics.hh: , I could not understand how the function computeOmega calculates the omega_{total} where the code is
[code=“cpp”]
static T computeOmega(T omega0, T preFactor, T rhoBar, Array<T,SymmetricTensor<T,Descriptor>::n> const& PiNeq)
{
T PiNeqNormSqr = SymmetricTensor<T,Descriptor>::tensorNormSqr(PiNeq);
T PiNeqNorm = std::sqrt(PiNeqNormSqr);
T alpha = preFactor * Descriptor::invRho(rhoBar);
T linearTerm = alphaPiNeqNorm;
T squareTerm = (T)2alphaalphaPiNeqNormSqr;
// In the following formula, the square-root appearing in the explicit form of
// omega is developed to second-order.
return omega0*(1-linearTerm+squareTerm);
}
.
This calculation seems to be a different form compared to the one in the paper by Hou, et al. (1994)[sup][1][/sup] or the one by Krafczyk 2003[sup][2][/sup]. If so, what is the benefits of this form?
Could anyone help explain this or provide any reference?
Thank you in advance.
With best,
Song
[1] Hou, et al. 1994, "A lattice Boltzmann subgrid model for high Reynolds number flows"
[2] Krafczyk 2003 "LARGE-EDDY SIMULATIONS WITH A MULTIPLE-RELAXATION-TIME LBE MODEL"