Hi,
I have a question about the way that the density is updated in VelocityDirichletBoundaryDynamics.
The function VelocityDirechletBoundaryDynamics::computeRhoBar() finally returns
T rhoBar =((T)2*rhoNormal+rhoOnWall-Descriptor<T>::SkordosFactor()*velNormal)
/ ((T)1+velNormal);
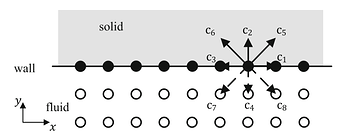
Considering the following case (copied for Kruger’s book),
it should give,
rho = [f0+f1+f3 + 2(f2+f5+f6)] / (1+velNormal)
where f0+f1+3 =
rhoOnWall and f2+f5+f6 = rhoNormal, which leads torho = (2*rhoNormal + rhoOnWall) / (1+velNormal)
Based on that rhoBar = rho - 1.
rhoBar = (2*rhoNormal + rhoOnWall - 1 - velNormal) / (1+velNormal)
which is different with the one implemented in the code.
rhoBar = (2*rhoNormal + rhoOnWall - SkordosFactor * velNormal) / (1+velNormal)
So here I have two main questions,
- What is SkordosFactor()? It seems always to be one as set in
src/latticeBoltzmann/roundOffPolicy.h. - Where does the difference come from?
Thank you!
Regards,
Song